链表

单链表反转

func reverseList(head *node)*node{   //第一种方法，利用Go的多个一起赋值
	cur:=head  //当前结点
	var pre *node=nil
	for cur!=nil{
		pre,cur,cur.next=cur,cur.next,pre
	}
	return pre
}

func reverseList02(head *node)*node{  //迭代循环来反转

	nextNode:=new(node)
	preNode:=new(node)
	nextNode=nil
	preNode=nil

	for head!=nil{
		nextNode=head.next   //先保存链表的下一个=
        
		head.next=preNode   //反转

		preNode=head   //相当于往下跑一个

		head=nextNode   //head也要往后面跑

	}

	return preNode
}

func recursiveTreverse(node *node){    //递归来反转
	if node==nil{
		return    //出口
	}
	if node.next==nil{
		endnode=node
		newlist=node
		return     //出口
	}

	recursiveTraverse(node.next)

	endnode.next=node   //反转
	endnode=node   //相当于下移
	endnode.next=nil  //最后需要尾指针
}

链表中环的检测

func IsLoop(head *Node)bool{
	fast:=new(Node)  //快指针
	slow:=new(Node)  //慢指针
	fast=head
	slow=head   //指向头结点

	for slow!=nil&&fast.Next!=nil{
		slow=slow.Next       //慢指针走一步
		fast=fast.Next.Next  //快指针走两步

		if fast==slow{   //有环 ，如果有环迟早会相遇
			return true
		}
	}

	return false
}

环长度检测

func listLoopEn(head *Node)*Node{   //寻找链表的环的入点
	fast:=new(Node)  //快指针
	slow:=new(Node)  //慢指针
	fast=head
	slow=head   //指向头结点

	for slow!=nil&&fast.Next!=nil{
		slow=slow.Next
		fast=fast.Next.Next  //快指针走两步

		if fast==slow{   //有环
			break    //记录相遇的点
		}
	}
	if slow==nil||fast.Next==nil{
		return nil    //说明不存在环，直接返回
	}
	ptr1:=new(Node) //指向第一个结点
	ptr2:=new(Node) //指向之前相遇的结点
	ptr1=head
	ptr2=slow
	
	for ptr1!=ptr2{
		ptr1=ptr1.Next
		ptr2=ptr2.Next   //一直向下走一步一步
	}
	return ptr1   //返回这个相遇的点，就是环的入口的点

}

func ListLoopLength(head *Node)int{   //环长度检测
	//求出环的长度
	//思路1：记录下相遇节点存入临时变量tempPtr，然后让slow(或者fast，都一样)
	// 继续向前走slow = slow -> next；一直到slow == tempPtr; 此时经过的步数就是环上节点的个数；
	//思路2： 从相遇点开始slow和fast继续按照原来的方式向前走slow = slow -> next; fast = fast -> next -> next；
	// 直到二者再次项目，此时经过的步数就是环上节点的个数 。
	fast:=new(Node)  //快指针
	slow:=new(Node)  //慢指针
	fast=head
	slow=head   //指向头结点
	tmp:=new(Node)   //保存临时点
	var length int
	for slow!=nil&&fast.Next!=nil{
		slow=slow.Next
		fast=fast.Next.Next  //快指针走两步

		if fast==slow{   //有环
			tmp=slow
			break
		}
	}
	length++
	tmp=tmp.Next  //先向前走一步
	for tmp!=slow{
		tmp=tmp.Next
		length++
	}
	return length
}

1 2	//求链表长度， //可以根据前面求出的条件求出起点到入口的距离然后加上环的长度，就是链表的长度

//求出环上距离任意一个节点最远的点（对面节点）
//对于换上任意的一个点ptr0, 我们要找到它的”对面点“，可以这样思考：同样使用上面的快慢指针的方法，让slow和fast都指向ptr0，每一步都执行与上面相同的操作（slow每次跳一步，fast每次跳两步），

//当fast = ptr0或者fast = prt0->next的时候slow所指向的节点就是ptr0的”对面节点“。

//对于问题6（扩展）如何判断两个无环链表是否相交，和7（扩展）如果相交，求出第一个相交的节点，其实就是做一个问题的转化：
//设有连个链表listA和listB，如果两个链表都无环，并且有交点，那么我们可以让其中一个链表（不妨设是listA）的为节点连接到其头部，这样在listB中就一定会出现一个环。

//因此我们将问题6和7分别转化成了问题1和2.

两个有序的链表合并

//递归的方法
func MergeList(L1 *Node,L2 *Node )*Node{  //有序合并两个单链表

	if L1==nil&&L2==nil{
		return nil   //两个都为空就返回nil
	}
	if L1==nil{
		return L2   //l1为空就返回l2
	}
	if L2==nil{
		return L1   //l2为空就返回l1
	}
	NewList:=new(Node)  //新的链表
	if L1.value>L2.value{
		NewList=L2
		NewList.Next=MergeList(L1,L2.Next)   //这里递归操作
	}else{
		NewList=L1
		NewList.Next=MergeList(L1.Next,L2)   //递归
	}
	return NewList
}

//循环方法来实现单链表合并
func MergeList02(L1 *Node,L2 *Node)*Node{   //普通循环遍历

	NewList:=new(Node)
	NewList.Next=nil  //创建新链表

	p1:=new(Node)  //声明两个指针分别指向两个链表的数据开始部分
	p2:=new(Node)
	p1=L1
	p2=L2

	last:=new(Node)   //声明一个指针指向新链表的最后一个结点，
	last=NewList

	for p1!=nil&&p2!=nil{

			if p1.value<p2.value{ //p1结点的数据小，last指向p1结点，然后向后移
				last.Next=p1
				p1=p1.Next
				last=last.Next
			}else{  //p2结点的数据小，last指向p2结点，然后向后移
				last.Next=p2
				p2=p2.Next
				last=last.Next
			}
	}
	//当有一个链表结束时，将last指向另外一条链表
	if p1==nil{
		last.Next=p2
	} else if p2==nil{
		last.Next=p1
	}
	return NewList
}

删除链表倒数第 n 个结点

//用快慢指针来实现
/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func removeNthFromEnd(head *ListNode, n int) *ListNode {
    
    if n<=0||head==nil{
        return head
    }
    //定义快慢指针，利用快慢指针来实现删除倒数第几个结点
    fast:=new(ListNode)   //快指针
    slow:=new(ListNode)   //慢指针
  //  list:=new(ListNode)
   
    fast=head
    slow=head
    
    for i:=0;i<n;i++{
        fast=fast.Next   //快指针先走完需要走的步数
    }
    if fast==nil{
        return head.Next
    }
    
    for fast.Next!=nil{
        slow=slow.Next
        fast=fast.Next   //一起走，等到快指针到结尾
    }
    
    slow.Next=slow.Next.Next
    return head
}

求链表的中间结点

1	//用快慢指针来实现，快指针走2步，慢指针走一步，快指针到底，慢指针就是中间结点

链表相关：：206，141，21，19，876 （leetcode）

栈

顺序栈（数组实现）
链式栈（链表实现）

栈相关：20,155,232,844,224,682,496. (leetcode)

队列

顺序队列（数组实现）
链式队列（链表实现）
循环队列，队满（(tail+1)%n=head），队空（head=tail）
阻塞队列

应用：

线程池池结构
生产者消费者模型
线程安全的队列我们叫作并发队列。最简单直接的实现方式是直接在enqueue()、dequeue() 方法上加锁，但是锁粒度大并发度会比较低，同一时刻仅允许一个存或者取操作。实际上，基于数组的循环队列，利用 CAS 原子操作，可以实现非常高效的并发队列。这也是循环队列比链式队列应用更加广泛的原因。

递归

递归改写为非递归（迭代循环）
需要注意，堆栈溢出，重复计算（可以用散列表存储然后调用前对比）
环检测（判断递归最终条件）

排序

冒泡排序

//冒泡排序
func BubbleSort(a []int)[]int{
    length:=len(a)  //求输出长度
    for i:=0;i<length-1;i++{
        for j:=0;j<length-i-1;j++{
            if a[j]>a[j+1]{
                a[j],a[j+1]=a[j+1],a[j]   //交换
            }
        }
    }
    return a
}

插入排序

func InsertSort(a []int)[]int{    //插入排序

	var tmp,j int    //零时变量
	for i:=1;i<len(a);i++{   //遍历后面的无序数组，先取第一个为有序数组
		if a[i]<a[i-1]{  //无序组第一个小于有序组最后一个进入
			tmp=a[i]    //取出这个带插入的数据
			for j=i-1;j>=0&&a[j]>tmp;j--{  //寻找待插入的位置,j需要大于0而且那个元素大于待插                                                   入的数据就继续循环，否则就是找到坑位
 				a[j+1]=a[j]    //向后面挪坑位
			}
			a[j+1]=tmp   //填入坑位，因为上面经过了j--，所以这里是j+1
		}
	}
	return a
}

归并排序

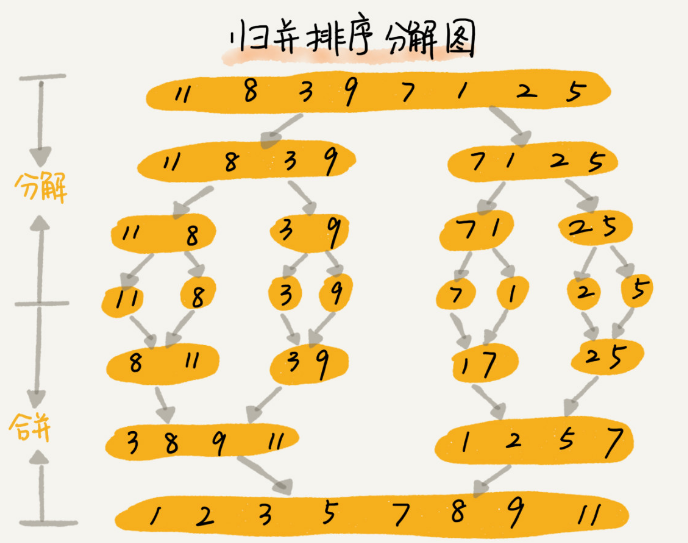
func MergeSort(a []int,length int){   //传入需要排序的切片和个数
	MergeSortR(a,0,length-1)   //需要用到递归
}
func MergeSortR(a []int,start,end int){  //传入需要排序的数据切片，还有起点和终点
	if start>=end{
		return    //递归结束的标志
	}
	midPoint:=(start+end)/2    //取起点到终点的中间位置，分开治理
	MergeSortR(a,start,midPoint) //起点到中间位置继续分治
	MergeSortR(a,midPoint+1,end) //中点到末尾分治
	MergeNum(a,start,midPoint,end)

}
func MergeNum(a []int,start,mid,end int){   //用来有序合并两个分组数据
	//开辟两个临时切片
	leftLengh:=mid-start+1
	rightLengh:=end-mid

	leftArr:=make([]int,leftLengh+1)
	rightArr:=make([]int,rightLengh+1)   //开辟两个临时切片，多加一个容量用于哨兵

	for i:=0;i<leftLengh;i++{
		leftArr[i]=a[start+i]    //拷贝到临时切片里面
	}
	leftArr[leftLengh]=8888    //哨兵，相当于标志位
	for i:=0;i<rightLengh;i++{
		rightArr[i]=a[mid+i+1]    //拷贝到临时切片
	}
	rightArr[rightLengh]=8888    //哨兵，相当于标志位

	i,j:=0,0   //两个标志指针
	for k:=start;k<=end;k++{   //遍历
		if leftArr[i]<rightArr[j]{  //小的先添加进去
			a[k]=leftArr[i]
			i++
		}else{
			a[k]=rightArr[j]
			j++
		}
	}
}

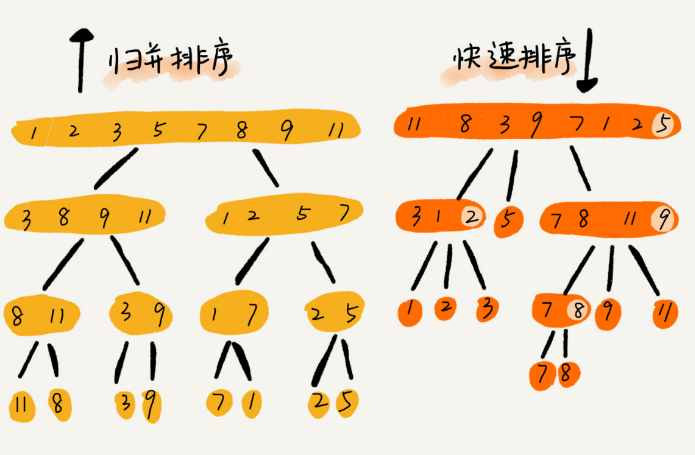
快速排序

func QuiteSort(a []int,length int){   //快速排序,传入切片和长度
	QuiteSortREC(a,0,length-1)    //递归函数
}
func QuiteSortREC(a[]int,start,end int){
	if start>=end{
		return    //递归结束的标志
	}
	pivot:=partition(a,start,end)    //获取分区点
	QuiteSortREC(a,start,pivot-1)
	QuiteSortREC(a,pivot+1,end)   //递归

}
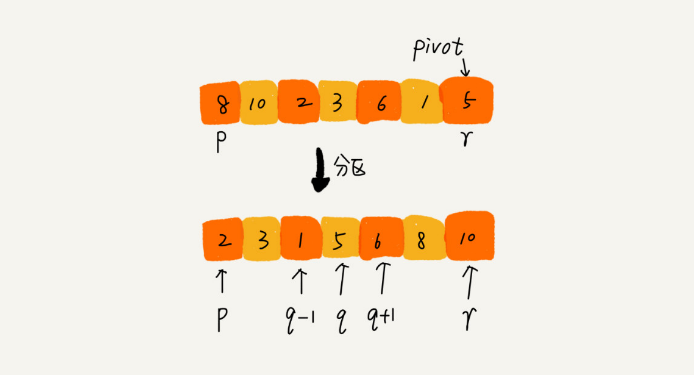
func partition(a []int,start,end int)int{//获取分区点，并且分区
	poivt:=a[end]    //先去取最后一个为分区点
	i:=start          //标记第一个开始点

	for j:=start;j<=end-1;j++{
		if a[j]<poivt{
			a[i],a[j]=a[j],a[i]    //交换
			i++          //标记后移
		}
	}
	a[i],a[end]=a[end],a[i]
	return i
}

二分查找

//简单非递归实现
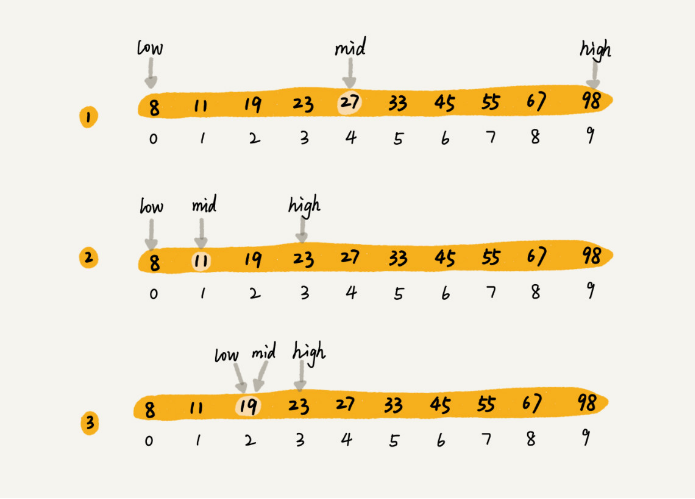
func BinarySearch(a []int,lengh,value int )int{   //二分查找飞递归简单实现
	low,high:=0,lengh-1      //头和尾
	for low<=high{
		mid:=low+((high-low)>>1)   //中间位置
		if a[mid]==value{
			return mid
		}else if a[mid]<value{    //中间值小于需要查找的值那么就往后移动空间
			low=mid+1
		}else{        //中间值大于需要查找的值那么就往前移动空间
			high=mid-1
		}
	}
	return -1    //如果没找到最后返回-1
}

func BinarySearchREC(a []int,low,high ,value int)int{   //递归实现
	if low>high{
		return -1    //这里说明没有找到
	}
	mid:=low+((high-low)>>1)
	if a[mid]==value{
		return mid
	}else if a[mid]<value{
		return BinarySearchREC(a,mid+1,high,value)     //递归进去
	}else{
		return BinarySearchREC(a,low,mid-1,value)     //递归进去
	}
}

二分查找变种

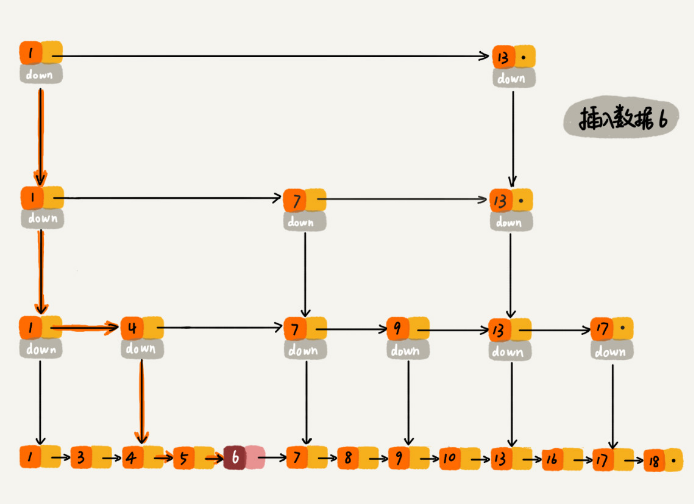
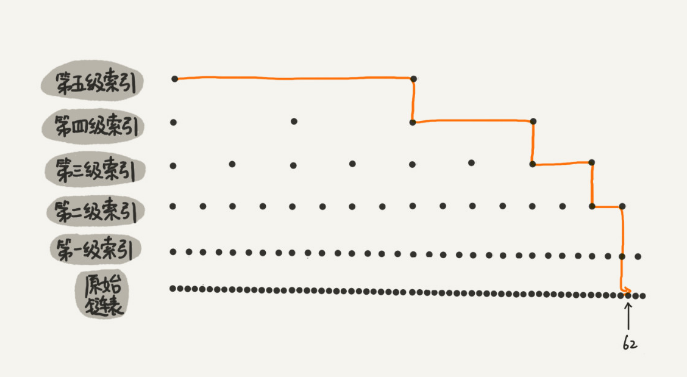
跳表
散列表

二叉树

//简单的三种遍历
type TreeNode struct{
	Left *TreeNode
	value interface{}
	Right *TreeNode
}

func (node *TreeNode)Print(){
	fmt.Println(node.value)    //打印结点值
}

//前序遍历
func (node *TreeNode)preOrder(){
	if node==nil{
		return
	}
	//根左右
	node.Print()
	node.Left.preOrder()
	node.Right.preOrder()
}

//中序遍历
func (node *TreeNode)middleOrder(){
	if node==nil{
		return
	}
	//左根右
	node.Left.middleOrder()
	node.Print()
	node.Right.middleOrder()
}

//后序遍历
func (node *TreeNode)postOrder(){
	if node==nil{
		return
	}
	//左右跟
	node.Left.postOrder()
	node.Right.postOrder()
	node.Print()
}

func CreatNode(value interface{})*TreeNode{
	return &TreeNode{nil,value,nil}
}
func main(){
	root:=CreatNode("root")
	root.Left=CreatNode("root-left-1")
	root.Right=CreatNode("root-right-1")
	root.Left.Left=CreatNode("root-left-left-1")
	root.Left.Right=CreatNode("root-left-right-1")
	root.Right.Left=CreatNode("root-right-left-1")
	root.Right.Right=CreatNode("root-right-right-1")
	root.postOrder()
}

1	//层次遍历，也就是广度优先遍历，可以借用队列的数据结构

二叉查找树

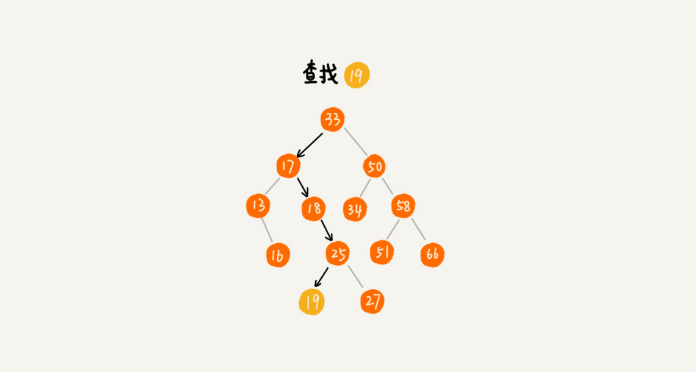
首先，我们看如何在二叉查找树中查找一个节点。我们先取根节点,如果它等于我们要查找的数据，那就返回。如果要查找的数据比根节小，那就在左子树中递归查找；如果要查找的数据比根节点的值大，那就在右子树中递归查找。

//二叉查找树的查找
type TreeNode struct{
	Left *TreeNode
	value interface{}
	Right *TreeNode
}
func (root *TreeNode)NodeFind(data int)*TreeNode{   //二叉查找树查找一个结点
	p:=root
	for p!=nil{    //刚开始指向二叉查找树的根节点
		if p.value.(int)==data{    //存储的时候是空接口，所以要类型断言
			return p
		}else if p.value.(int)>data{
			p=p.Left     //
		}else {
			p=p.Right
		}

	}
	return nil   //如果这里返回就是没找到
}

二叉查找树的插入

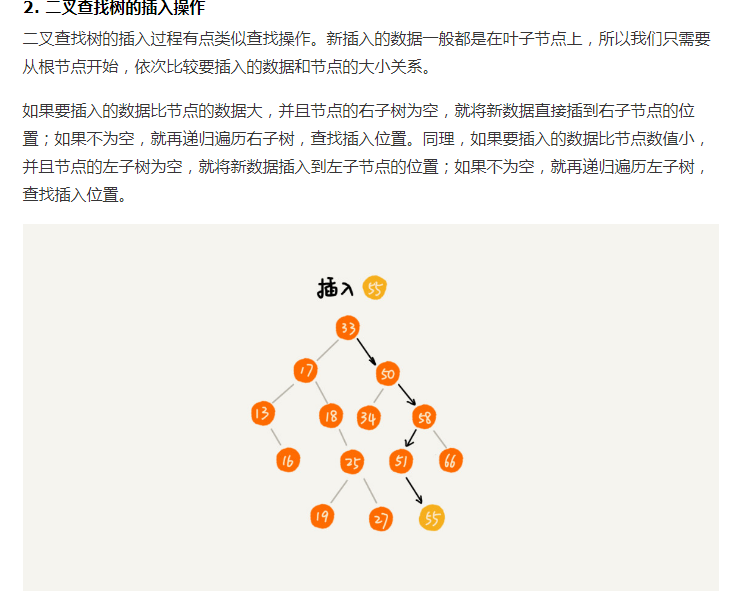
func (root *TreeNode)Insert(data int){   //二叉查找树的插入,默认树不位空
	p:=root
	for p!=nil{
		if data>p.value.(int){   //放在右子树
			if p.Right==nil{  //如果右子树结点为空那么就直接插入
				p.Right=&TreeNode{nil,data,nil}  //插入
				return 
			}else{    //右子数不位空
				p=p.Right  //继续想右寻找
			}
		}else{   //放在左子树
			if p.Left==nil{
				p.Left=&TreeNode{nil,data,nil}//插入
				return
			}else{
				p=p.Left
			}
		}
	}

}

二叉查找树的删除

func (root *TreeNode)Delete(data int){   //二叉查找树的删除
	p:=root   //初始化指向根节点
	pp:=&TreeNode{nil,nil,nil}  //用来记录p结点的父节点，初始化为空

	//先寻找到那个结点位置
	for p!=nil&&data!=p.value.(int){
		pp=p
		if data>p.value.(int){
			p=p.Right
		}else{
			p=p.Left
		}
	}
	if p==nil{
		return   //如果p一直循环到空,那么说明没有找到
	}

	//要删除的结点有两个子节点
	if p.Right!=nil&&p.Left!=nil{
		minp:=p.Right
		minpp:=p   //minpp代表minp的父节点
		//找到有子树中最小的
		for minp!=nil{
			minpp=minp
			minp=minp.Left
		}
	p.value=minp.value  //将右子树中最小的值替换到要删除的那里
	p=minp  //下面就变成删除minp了
	pp=minpp
	}

	//删除的结点是叶子结点或者是只有一个子结点
	child:=&TreeNode{nil,nil,nil}//用来记录子结点
	if p.Left!=nil{   //说明左结点不为空
		child=p.Left
	}else if p.Right!=nil{
		child=p.Right
	}else{
		child=nil
	}

	if pp.Left==p{
		pp.Left=child   //直接指向p的子结点
	}else{
		pp.Right=child
	}

}

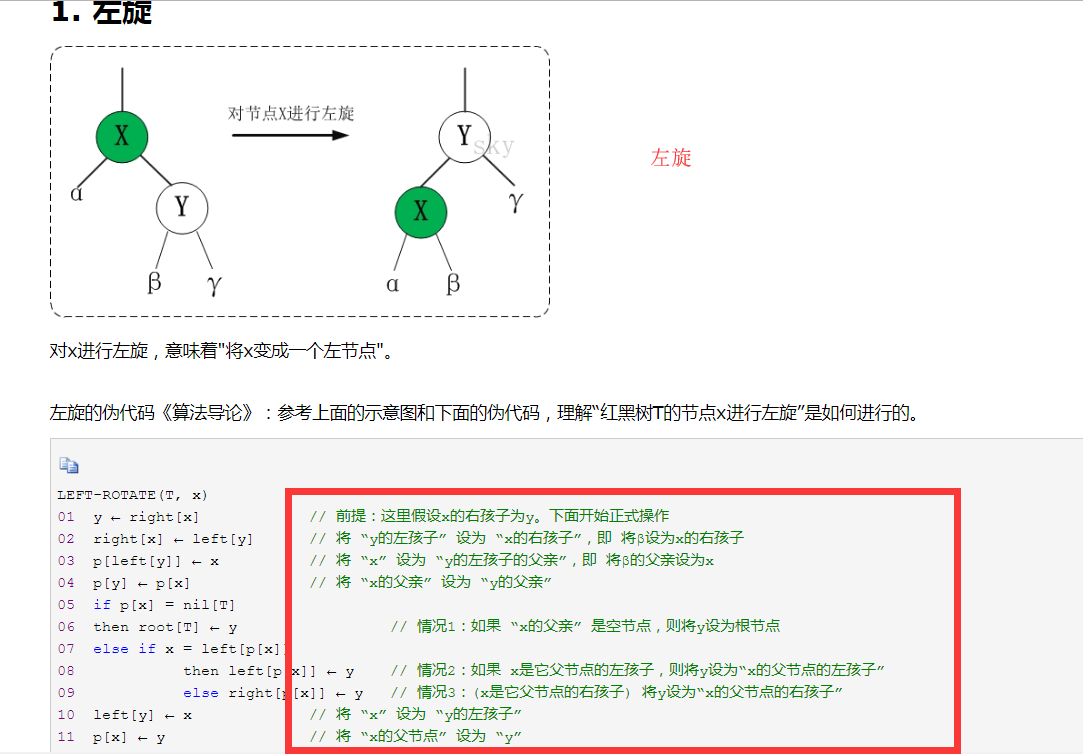
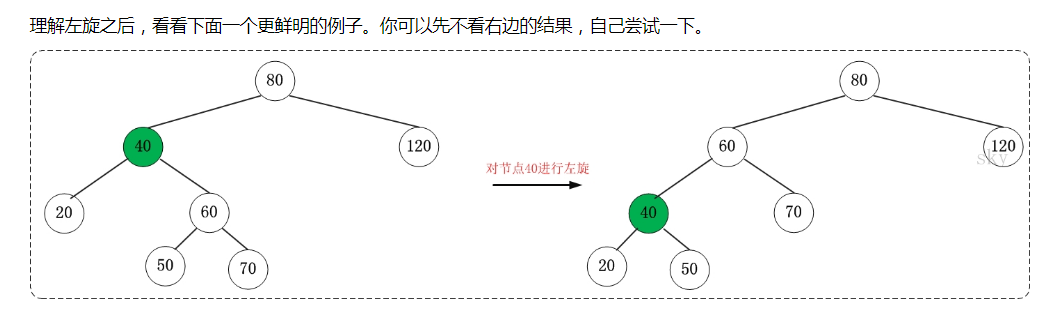
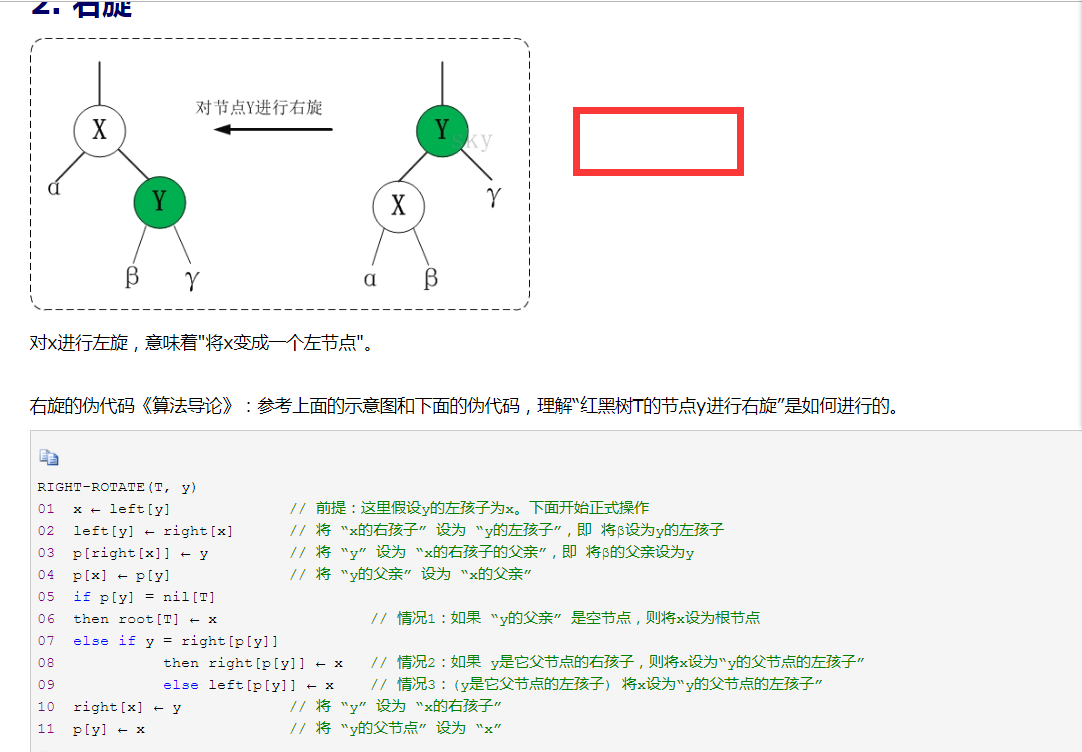
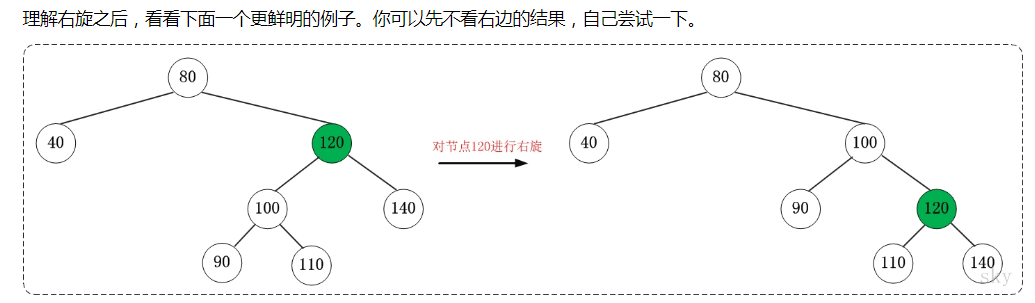
红黑树